다익스트라 알고리즘은 그래프에서 출발점에서 목표점 까지의 최단거리를 구할 때 사용하는 알고리즘이다.
이 때의 그래프의 가중치는 양수여야만 한다. 음수인 경우에는 벨만 포드 알고리즘을 사용해야한다.
동작순서는 다음과 같다.
1. 방문하지 않은 정점 중에서 그 거리가 최소인 점 x을 선택한다.
2. x를 방문 처리한다.
3. x와 연결된 정점들을 검사한다.
4. x와 연결된 정점들까지의 거리가 x를 거쳐 그 점까지의 거리와 비교해서 더 크다면 후자를 전자에 삽입한다.
5. 1~4 반복
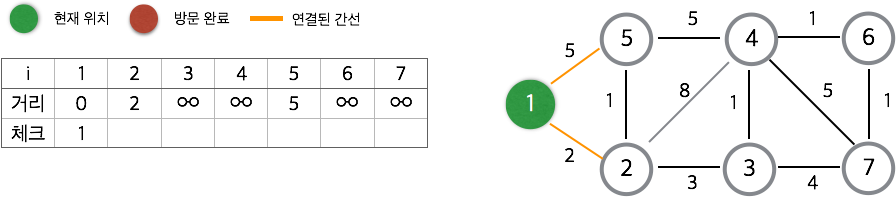
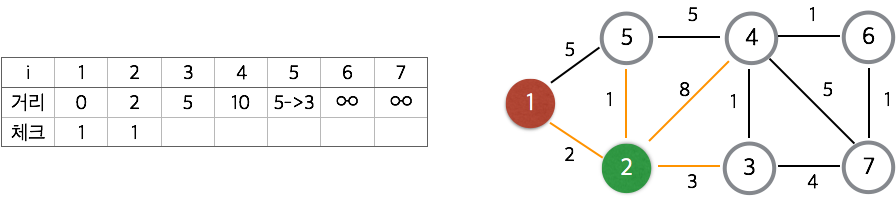
다음과 같이 진행된다.
구현코드는 다음과 같다.
동작원리를 외워두는 것이 좋다.
특정 문제에서는 간선의 방향성이 주어지기도 하고, 갈 수 없는 점이 나오기도 하기 때문이다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
|
class test{
static int v;
static int e;
static final int inf=1000000;
public static void main(String[] args) throws IOException {
Scanner sc = new Scanner(System.in);
v = sc.nextInt();
e = sc.nextInt();
int[][] ad = new int[v+1][v+1];
int[] dist = new int[v+1];
boolean[] visit = new boolean[v+1];
int start = sc.nextInt();
for (int i = 0; i < e; i++) {
int a = sc.nextInt();
int b = sc.nextInt();
int c = sc.nextInt();
ad[a][b] = c;
}
for (int i = 1; i <= v; i++)
dist[i]=inf;
solution(start, dist, ad, visit);
}
public static void solution(int start, int[] dist, int[][] ad, boolean[] visit) {
dist[start] = 0;
String s="";
for (int i = 0; i < v; i++) {
int min = inf + 1;
int idx = -1;
for (int j = 1; j <= v; j++) {
if (!visit[j] && min > dist[j]) {
min = dist[j];
idx = j;
}
}
visit[idx] = true;
s+=idx+" ";
for (int j = 1; j <= v; j++) {
if (ad[idx][j] != 0 && dist[j] > dist[idx] + ad[idx][j]) {
dist[j] = dist[idx] + ad[idx][j];
}
}
}
for (int i = 1; i <=v; i++) {
if(dist[i]==inf) System.out.println("INF");
else System.out.println(dist[i]);
}
}
}
|
cs |
우선순위 큐를 사용하여 구현하면 다음과 같다
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
|
import java.util.*;
class Element implements Comparable<Element>{
int idx;
int distance;
Element(int idx, int distance){
this.idx = idx;
this.distance = distance;
}
@Override
public int compareTo(Element o) {
return this.distance - o.distance;
}
}
public class test {
static boolean[] visit;
static int[] dist;
static int[][] ad;
static int v, e;
static final int inf = 100000;
public static void dijkstra(int start){
PriorityQueue<Element> que = new PriorityQueue<>();
dist[start] = 0;
que.offer(new Element(start, dist[start]));
while(!que.isEmpty()){
Element tmp = que.poll();
int distance = tmp.distance;
int idx = tmp.idx;
if(distance > dist[idx])
continue;
for(int i = 1; i <= v; i++){
if(ad[idx][i] != 0 && dist[i] > dist[idx] + ad[idx][i]){
dist[i] = dist[idx] + ad[idx][i];
que.add(new Element(i, dist[i]));
}
}
}
System.out.println();
for(int i =1 ; i <= v; i++){
System.out.print(dist[i]+" ");
}
}
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
v = sc.nextInt();
e = sc.nextInt();
visit = new boolean[v+1];
dist = new int[v+1];
ad = new int[v+1][v+1];
for(int i = 0; i <= v; i++){
dist[i] = inf;
}
for(int i = 0; i < e; i++){
int a = sc.nextInt();
int b = sc.nextInt();
int c = sc.nextInt();
ad[a][b] = c;
ad[b][a] = c;
}
dijkstra(1);
}
}
|
cs |
'Java' 카테고리의 다른 글
| Java EOF(End Of File) 처리하기 (0) | 2020.09.11 |
|---|---|
| Java System.arraycopy() 에 대해 (0) | 2020.09.11 |
| Java 프림 알고리즘(Prim Algorithm)과 크루스칼 알고리즘(Kruskal Algorithm)에 대해 (0) | 2020.09.07 |
| 자바에서 volatile 이란? (0) | 2020.09.04 |
| 위상정렬 자바로 구현하기, 백준2252_줄 세우기 (0) | 2020.08.31 |
