Java 프림 알고리즘(Prim Algorithm)과 크루스칼 알고리즘(Kruskal Algorithm)에 대해

프림 알고리즘과 크루스칼 알고리즘은 MST(Minimum Spanning Tree)를 구하는 알고리즘이다. 

 

Spanning Tree 란 그래프 중 모든 정점이 간선으로 연결되어 있으면서 싸이클이 없는 그래프를 의미한다.

 

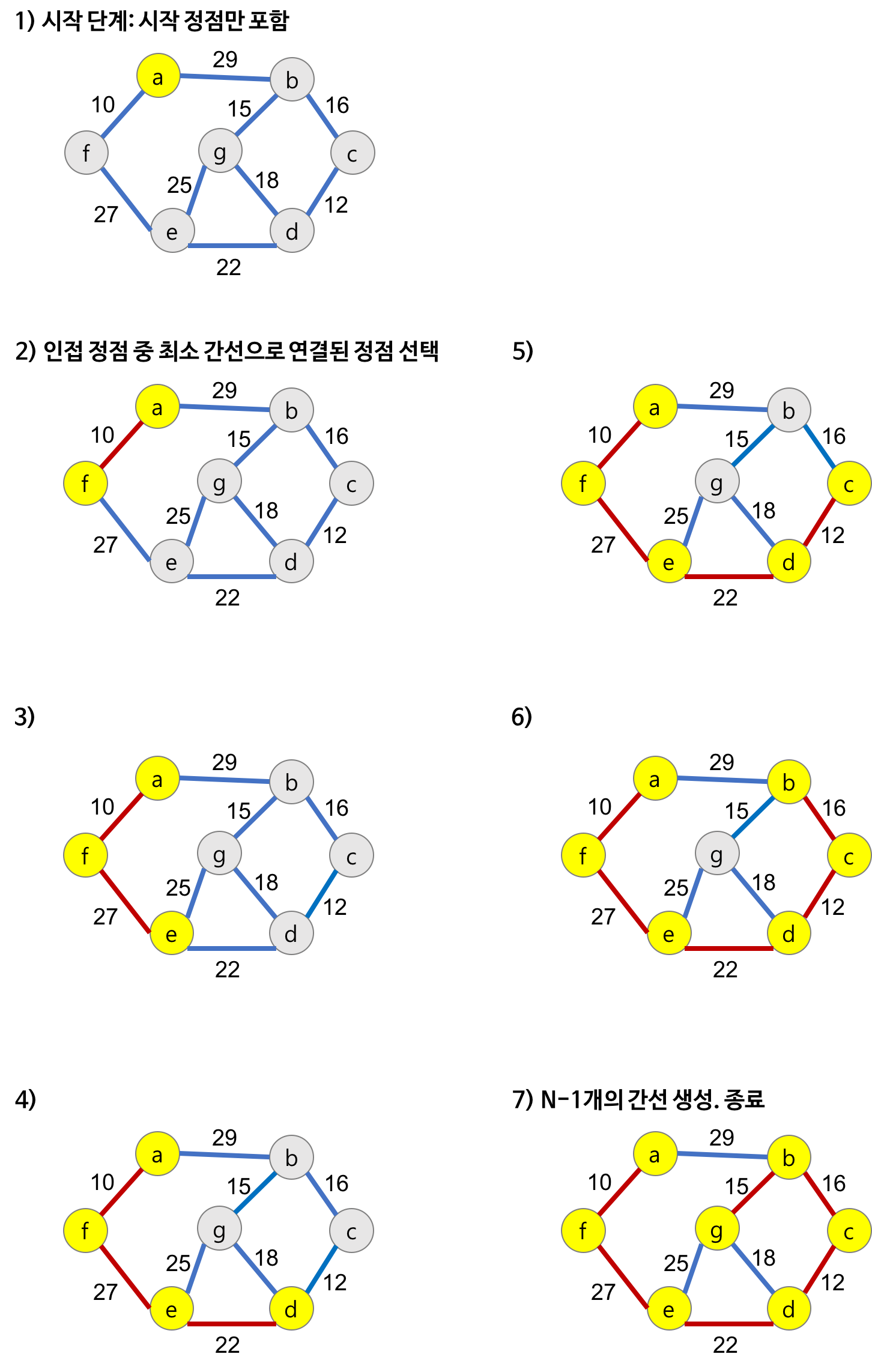
Prim 알고리즘은 시작 정점에서부터 출발해서 신장트리 집합을 단계적으로 확장해나가는 방법이다.

 

동작 순서

1. 시작 단계에서는 시작 정점만이 MST 집합에 포함된다.

2. 앞 단계에서 만들어진 MST 집합에 인접한 정점들 중에서 최소 간선으로 연결된 정점을 선택하여 트리를 확장한다.

3. n-1 개의 간선이 될 때까지 반복한다.

이미지 출처 : https://gmlwjd9405.github.io/2018/08/30/algorithm-prim-mst.html

 

 

 

Kruskal 알고리즘은 간선 선택을 기반으로 하는 알고리즘이다.

 

동작 순서

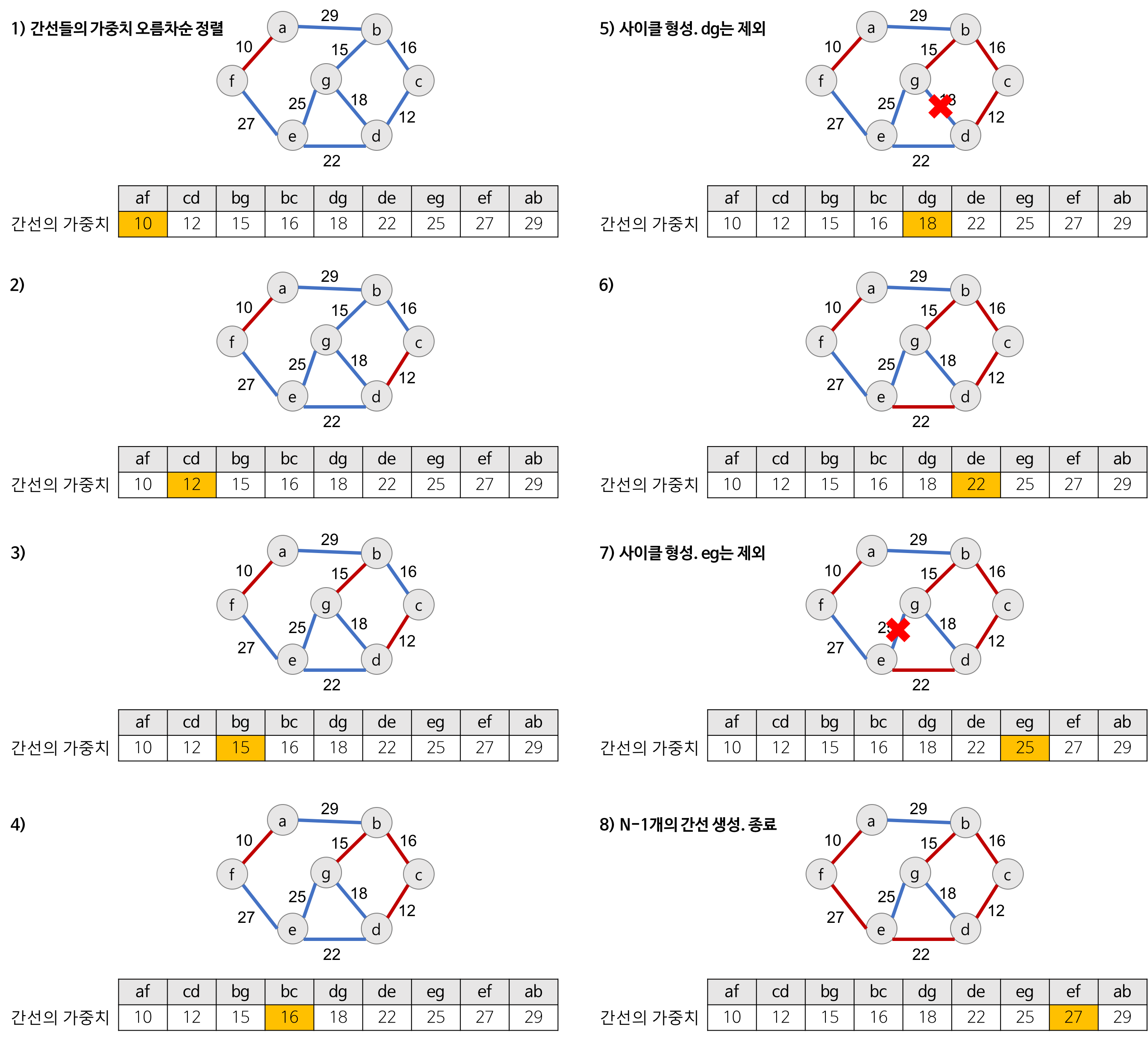
1. 그래프의 간선들을 가중치의 오름차순으로 정렬한다.

2. 정렬된 간선 리스트에서 순서대로 사이클을 형성하지 않는 간선을 선택한다.

  ( 가장 낮은 가중치부터 선택하고 그 간선을 선택했을 때에 사이클을 형성하면 건너뛴다 )

3. 해당 간선을 현재의 MST의 집합에 추가한다.

 

여기서 싸이클 형성 여부는 유니온 파인드 알고리즘을 사용한다.

이미지 출처 : https://gmlwjd9405.github.io/2018/08/29/algorithm-kruskal-mst.html

 

 

Prim은 O(n^2)

Kruskal은 O(elog2e) 이므로

적은 숫자의 간선만을 가지는 희소 그래프의 경우 Kruskal,

그래프에 간선이 많이 존재하는 밀집 그래프의 경우는 Prim 이 적합하다.

 

크루스칼 알고리즘은 탐욕적인 방법을 이용해서 그래프의 모든 정점을 최소 비용으로 연결하는 답을 구하는 것이다.

탐욕적 방법은 그 순간에는 최적이지만, 전체적인 관점에서 최적이라는 보장이 없어서 검증을 해야하지만, 크루스칼 알고리즘은 최적의 해답을 주는 것으로 증명되어있다고 한다.

 

유니온 파인드에 대해서는

ssungkang.tistory.com/entry/Algorithm-%EC%9C%A0%EB%8B%88%EC%98%A8-%ED%8C%8C%EC%9D%B8%EB%93%9CUnion-Find

[Algorithm] 유니온 파인드(Union - Find)

설명을 너무 잘해놓은 티스토리가 있어 링크를 남긴다.

 

유니온 파인드 구현

 

public class test{
    public static void main(String[] args) throws IOException {
        int[] parent=new int[9];
        Arrays.fill(parent, -1);
        union(parent, 1, 2);
        union(parent, 2, 3);
        union(parent, 3, 4);
        union(parent, 4, 5);
        union(parent, 6, 6);
        union(parent, 7, 8);
        System.out.println(isCycle(parent, 1, 4));
    }
 
    public static int find(int[] parent, int a) {
        if (parent[a] < 0) {
            return a;
        } else {
            return parent[a] = find(parent, parent[a]);
        }
    }
 
    public static void union(int[] parent, int x, int y) {
        x = find(parent, x);
        y = find(parent, y);
        if(x==y) return;
        if (parent[x] < parent[y]) {
            parent[x] += parent[y];
            parent[y] = x;
        } else {
            parent[y] += parent[x];
            parent[x] = y;
        }
    }
 
    public static boolean isParent(int[] parent, int x, int y) {
        int a = find(parent, x);
        int b = find(parent, y);
        return a==b;
    }
}

 

프림 알고리즘 구현 (프로그래머스 섬연결하기 문제를 프림 알고리즘으로 풀어봄)

 

    public static class Edge implements Comparable<Edge> {        public int from;        public int to;        public int weight;        public Edge(int from, int to, int weight) {            this.from = from;            this.to = to;            this.weight = weight;        }        @Override        public int compareTo(Edge o) {            return this.weight - o.weight;        }    }    public static int solution(int n, int[][] costs) {        int totalWeight = 0;        int[] parent = new int[n];        List<Edge> edges = new ArrayList<>();        Arrays.fill(parent, -1);        for (int[] cost : costs) {            edges.add(new Edge(cost[0], cost[1], cost[2]));        }        Collections.sort(edges);        for (Edge edge : edges) {            if (isCycle(edge.to, edge.from, parent)) {                continue;            }            totalWeight += edge.weight;            union(edge.to, edge.from, parent);        }        return totalWeight;    }    private static void union(int a, int b, int[] parent) {        int aRoot = find(a, parent);        int bRoot = find(b, parent);        if (aRoot == bRoot) {            return;        }        if (aRoot < bRoot) {            parent[bRoot] += parent[aRoot];            parent[aRoot] = bRoot;            return;        }        parent[aRoot] += parent[bRoot];        parent[bRoot] = aRoot;    }    private static boolean isCycle(int to, int from, int[] parent) {        return find(to, parent) == find(from, parent);    }    private static int find(int node, int[] parent) {        if (parent[node] < 0) {            return node;        }        return parent[node] = find(parent[node], parent);    }

유니온 파인드에서 조금만 변형을 해주면 된다.

ArrayList 대신 PriorityQueue를 이용해도 된다.